Induksi Matematika bagian keempat (Menginduksi Barisan Bilangan)

kkaktrichannel.info ~ Assalamualaikum Wr wb . INDUKSI MATEMATIKA, berikut ini adalah postingan kempat dari kkatri tentang Induksi Matematika, sebelumnya kaktri sudah memberikan materi dasar dan contoh-contoh induksi matematika di bagian 1, 2 dan 3. jika kalian belum menyimak dan membacanya silahkan kli link berikut ini :

1. Induksi Matematika Bagian 1 (lihat)

2. Induksi Matematika Bagian 2 (lihat)

3. Induksi Matematika Bagian 3.(lihat)

untuk bagian keempat ini kkatri akan membahas Induksi Matematika dalam bentuk Barisan Bilangan dan juga tentang keterbagian suatu rumus bilangan berpangkat. kkaktri akan membahas tenatng materi dan juga contoh soalnya, adapun penyajian secara lengkap di bahs di blog ini dan juga di channel youtube kkatri di channel youtube KECEVID, silahkan kunjungi channel youtube kkatri bila ingin melihat secara detail bagaimana kktri menjelaskan tentang Induksi Matematika yang kktri tulis di blog ini. berikut adalah materi dan Contoh Soal INDUKSI MATEMATIKA bagian keempat, silahkan membacanya dan menyimaknya dengan penuh semangat!.

Meskipun menentukan satu rumus yang berdasarkan beberapa pengamatan saja tidak menjamin kebenaran rumus tersebut, tetapi mengenali pola adalah hal yang penting. Ketika kita mendapatkan pola atau rumus yang kita pikir benar, kita dapat membuktikan kebenaran pola atau rumus tersebut dengan menggunakan induksi matematika.

Materi Mencari Rumus Suku ke-n Suatu Barisan

Untuk mencari rumus suku ke-n dari suatu barisan, perhatikan petunjuk berikut.

1. Hitung beberapa suku pertama dari barisan yang diberikan. Biasanya sangat membantu jika kita menulis suku-suku tersebut ke dalam bentuk sederhana dan bentuk faktor.

2. Cobalah untuk menemukan pola dari suku-suku yang telah kita hitung dan tulis rumus suku ke-n barisan tersebut. Rumus ini merupakan hipotesis atau konjektur kita. Mungkin kita perlu mencoba untuk menghitung satu atau dua suku selanjutnya dalam barisan tersebut untuk menguji hipotesis kita.

Contoh Soal dan Pembahasan Induksi Matematika

Gunakan induksi matematika untuk membuktikan hipotesis yang kita dapatkan.

Soal 14: Menemukan Rumus untuk Barisan Terhingga

Carilah rumus untuk penjumlahan berhingga berikut kemudian buktikan rumus tersebut dengan induksi matematika.

$\frac{1}{4}$ + $\frac{1}{12}$ + $\frac{1}{24}$ + ... +$\frac{1}{2n(n + 1)}$

Pembahasan Soal 14

Pembahasan Kita mulai dengan menuliskan beberapa penjumlahan pertama.

$S_1$ = $\frac{1}{4}$ = $\frac{1^2}{2(1)(1 + 1)}$

$S_2$ = $\frac{1}{4}$ + $\frac{1}{12}$ = $\frac{4}{12}$ = $\frac{2^2}{2(2)(2 + 1)}$

$S_3$ = $\frac{1}{4}$ + $\frac{1}{12}$  + $\frac{1}{24}$ = $\frac{9}{24}$ = $\frac{3^2}{2(3)(3 + 1)}$

$S_4$ = $\frac{1}{4}$ + $\frac{1}{12}$  + $\frac{1}{24}$ + $\frac{1}{40}$= $\frac{16}{40}$ = $\frac{4^2}{2(4)(4 + 1)}$

Dari barisan ini, tampak bahwa rumus penjumlahan k suku pertama adalah

$\frac{1}{4}$ + $\frac{1}{12}$ + $\frac{1}{24}$ + ... +$\frac{1}{2k(k + 1)}$ = $\frac{k^2}{2(k)(k + 1)}$

Untuk membuktikan kebenaran hipotesis ini, kita gunakan induksi matematika. Perhatikan bahwa kita telah menguji rumus ini untuk n = 1, sehingga kita mulai dengan menganggap bahwa rumus tersebut benar untuk n = k dan mencoba untuk menunjukkan bahwa rumus tersebut juga benar untuk n = k + 1.

$S_{k + 1}$ = [$\frac{1}{4}$ + $\frac{1}{12}$ + $\frac{1}{24}$ + ... +$\frac{1}{2k(k + 1)}$] + $\frac{1}{2(k+ 1)((k + 1) + 1)}$

$S_{k + 1}$ = $\frac{k^2}{2(k)(k + 1)}$ + $\frac{1}{2(k+ 1)(k + 2)}$

$S_{k + 1}$ = $\frac{k^2(k + 2) + k}{2(k + 1)(k + 2)}$

$S_{k + 1}$ = $\frac{k(k^2 + 2k + 1)}{2k(k + 1)(k + 2)}$

$S_{k + 1}$ = $\frac{(k + 1)^2}{2(k + 1)((k + 1) + 1)}$

Jadi, berdasarkan induksi matematika hipotesis tersebut benar.

Soal 15: Mencari Rumus untuk Barisan Terhingga

Carilah rumus untuk penjumlahan berhingga berikut kemudian buktikan rumus tersebut dengan induksi matematika.

$\frac{1}{2.3}$ + $\frac{1}{3.4}$ +  $\frac{1}{4.5}$ + ... + $\frac{1}{(n + 1)(n + 2)}$ 

Pembahasan 

Kita tulis beberapa penjumlahan pertama sebagai berikut.

$S_1$ = $\frac{1}{2.3}$ = $\frac{1}{6}$ = $\frac{1}{2(1 + 2)}$  

$S_2$ = $\frac{1}{2.3}$ + $\frac{1}{3.4}$ = $\frac{3}{12}$ =  $\frac{2}{8}$ =$\frac{2}{2(2 + 2)}$ 

$S_3$ = $\frac{1}{2.3}$ + $\frac{1}{3.4}$ + $\frac{1}{4.5}$= $\frac{18}{60}$ =  $\frac{3}{10}$ =$\frac{3}{2(3 + 2)}$ 

$S_4$ = $\frac{1}{2.3}$ + $\frac{1}{3.4}$ + $\frac{1}{4.5}$  + $\frac{1}{5.6}$= $\frac{20}{60}$ =  $\frac{4}{12}$ =$\frac{4}{2(4 + 2)}$ 

Berdasarkan pola di atas, kita dapat melihat bahwa rumus jumlah k suku pertama adalah

$S_k$= $\frac{1}{2.3}$ + $\frac{1}{3.4}$ + $\frac{1}{4.5}$ + ... + $\frac{1}{(k + 1).(k + 2)}$= $\frac{k}{2(k + 2)}$

Kita gunakan induksi matematika untuk membuktikan konjektur tersebut. Karena kita sudah menunjukkan kebenaran rumus tersebut untuk n = 1, kita mulai pembuktian ini dengan menganggap bahwa rumus ini benar untuk n = k, dan mencoba untuk menunjukkan bahwa rumus tersebut juga benar untuk n = k + 1.

$S_{k + 1}$= [$\frac{1}{2.3}$ + $\frac{1}{3.4}$ + $\frac{1}{4.5}$ + ... + $\frac{1}{(k + 1).(k + 2)}$] + $\frac{1}{((k+ 1) + 1) + ( (k +1) + 2)}$

$S_{k + 1}$= $\frac{k}{2(k + 2)}$ + $\frac{1}{(k + 2)(k + 3}$

$S_{k + 1}$= $\frac{k(k+3) + 2}{2(k + 2)(k +3)}$ 

$S_{k + 1}$= $\frac{k^2 + 3k + 2}{2(k + 2)(k +3)}$ 

$S_{k + 1}$= $\frac{(k + 1)(k +2)}{2(k + 2)(k +3)}$ 

$S_{k + 1}$= $\frac{(k + 1)}{2((k + 1) + 2)}$ 

Jadi, berdasarkan induksi matematika konjektur kita tersebut benar.

Soal 16: Membuktikan Keterbagian

Gunakan induksi matematika untuk menunjukkan bahwa $5^n$ – 1 habis dibagi 4 untuk semua bilangan bulat positif n.

Pembahasan

Untuk n = 1,

$5^1$ – 1= 4

yang sangat jelas habis dibagi 4.

Kita anggap $5^k$ – 1 habis dibagi 4 untuk sebarang bilangan bulat positif k. Akan kita tunjukkan $5^{k + 1}$ – 1 juga habis dibagi 4.

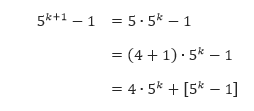
$5^{k + 1}$ – 1 = 5 . $5^k$ - 1

$5^{k + 1}$ – 1 = (4 + 1) . $5^k$ - 1

$5^{k + 1}$ – 1 = 4$5^k$ +( $5^k$ - 1)

Karena 4 ∙ $5^k$ dan $5^k$ – 1 habis dibagi 4 maka $5^{k+1}$– 1 habis dibagi 4. Jadi, kita dapat menyimpulkan bahwa $5^n$ – 1 habis dibagi 4 untuk semua bilangan bulat positif n.

Soal 17: Bilangan Ganjil

Buktikan bahwa n² – n + 41 merupakan bilangan ganjil untuk semua bilangan bulat positif n.

Pembahasan Soal 17

Untuk n = 1,

$1^2 - 1 + 41 = 41$

merupakan bilangan ganjil.

Kita anggap untuk sebarang bilangan bulat positif k, k² – k + 41 merupakan bilangan ganjil. Selanjutnya kita harus menunjukkan bahwa (k + 1)² – (k + 1) + 41 adalah bilangan ganjil.

$(k + 1)^2$ - (k + 1) + 41 = $k^2$ + 2k + 1 - k - 1 + 41

$(k + 1)^2$ - (k + 1) + 41 = ($k^2$ - k + 41) + 2k

Karena k² – k + 41 adalah bilangan ganjil dan 2k adalah bilangan genap, maka jumlah kedua bilangan tersebut, yaitu (k + 1)² – (k + 1) + 41 merupakan bilangan ganjil. Jadi, dengan menggunakan Prinsip Induksi Matematika kita dapat meyimpulkan bahwa n² – n + 41 merupakan bilangan ganjil untuk semua bilangan bulat positif n.

Soal 18: Membuktikan Induksi Matematika Keterbagian

Buktikan bahwa $3^{2n}$ – 1 habis dibagi 8 untuk semua bilangan bulat positif n.

Pembahasan 

Misalkan P(n) merupakan notasi untuk pernyataan “  $3^{2n}$ – 1  habis dibagi 8.”

Pertama kita tunjukkan bahwa P(1) benar. Karena

 $3^{2.1}$ – 1 = 8

yang habis dibagi 8, maka P(1) terbukti benar.

Anggap bahwa P(k) benar. Sehingga hipotesis induksi kita menyatakan bahwa  $3^{2k}$ – 1  habis dibagi 8. Selanjutnya kita akan tunjukkan bahwa P(k + 1) juga bernilai benar.

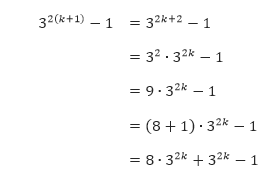
$3^{2(k+1)}$ – 1 =  $3^{2k+2}$ – 1

$3^{2(k+1)}$ – 1 =  $3^2.3^{2k}$ – 1

$3^{2(k+1)}$ – 1 =  $9.3^{2k}$ – 1

$3^{2(k+1)}$ – 1 =  $(8 + 1).3^{2k}$ – 1

$3^{2(k+1)}$ – 1 =  $8.3^{2k}$  +  $3^{2k}$ – 1

Karena 8 ∙  $3^{2k}$  dan  $3^{2k}$  – 1 habis dibagi 8 maka  $3^{2(k+1)}$ – 1 habis dibagi 8. Jadi dengan menggunakan induksi matematika kita dapat menyimpulkan bahwa  $3^{2n}$  – 1 habis dibagi dengan 8 untuk semua bilangan bulat positif n.

Soal Berikutnya Bagian 5

Demikianlah Pembahasan Soal Induksi Matematika bagian keempat (Menginduksi Barisan Bilangan). semoga bermanfaat